育種学会2015秋　若手の会ワークショップ

葉の輪郭形状解析

@(Chitwood2012)を例に，葉の輪郭形状解析からどのような生物学的・農学的知見が明らかにできるかを紹介した．
また，輪郭形状解析によく用いられる楕円フーリエ解析をFijiとRを利用しておこなう手順を例示した．
ここでは，FijiとRを利用した楕円フーリエ解析の流れをより具体的に解説する．

使うツールやデータ

Fiji

ImageJの生命科学系プラグインのバンドル版．今回は

領域分割
二値化
エッヂ検出

に用います．

参考:

インストール方法（Installation）
基本的な使い方（Tutorials）
様々なプラグイン（Plugins）

R

統計解析用プログラミング言語，またはその実装．
今回はR及びそのパッケージのMomocsを用いて，

エッヂ検出
楕円フーリエ解析
主成分分析
形態の再構築

をおこないます．

Momocs

主に輪郭形状解析を目的としたRのパッケージ．
現在も開発中ですので，開発者のGitHubレポジトリから最新版をインストールします．
GitHubからのインストールにはdevtools(GitHub,CRAN)を利用しますので，

WindowsではRtools
MacではXcode
Linuxでは各種コンパイラやライブラリ

がそれぞれ必要となります．

追記:Momocsの正式版がリリースされました．今後はCRANより他のパッケージ同様直接インストール可能ですが，最新版のインストールが開発者により推奨されています．

サンプルデータ

ワークショップではChitwood LabのWebページで公開しているトマトの野生種の画像データベースのサンプルを利用しました．
これらのデータは@(Chitwood2012)の解析に実際に用いられたデータセットです（著作権的な問題のため，データの転載はしません）．
~~興味がある方はChitwood LabのWild relatives of tomato | Databaseを参照して下さい．~~（現在は公開されていません）

代わりに，ここでは@(Chitwood2015)のブドウの野生種の葉の画像データの一部を楕円フーリエ解析の具体的な手順の説明に用います．

データはHarverd DataverseにてCC0で公開されています．

Climate and developmental plasticity: interannual variability in grapevine leaf morphology

ここでは，このデータセットから5枚の葉の画像を抜き出したサンプルデータを利用します．

解析手順

準備

サンプルデータとコード一式はこちら（noshita/wsJBS2015Aut|GitHub）からダウンロードできます．
これを解凍し，作業ディレクトリとします．
作業ディレクトリは，このような構成になっていると想定します．

wsJBS2015Aut
- img
  - grapevine オリジナル画像．Climate and developmental plasticity: interannual variability in grapevine leaf morphology(doi:10.7910/DVN/KOG6SY)のサブセット．
    - [Specimen Num].jpg
  - binarized 二値画像
    - [Specimen Num].jpg
- coord 各標本・各葉の輪郭の座標データ
  - [Specimen Num]_[Leaf Num].csv
- ij Fiji関連
  - classifiler_01.model Trainable Weka Segmentationの判別器．
  - classifiler_02.model 01より汎化させた判別器．
  - outlines.py 二値画像から輪郭の座標値を出力するPythonスクリプト．Fijiから呼び出し使う．
- efa.r 楕円フーリエ解析用Rスクリプト
- README.md

作業ディレクトリの構成を維持しておけば，作業ディレクトリ自体はどこに配置しても構いません．

Fijiでの前処理

画像をFijiに読み込み解析を開始します．
画像の取り込みはドラッグ&ドロップまたは「File」→「Open…」を選択し行います．

1. 領域分割と二値化

Fijiには幾つかの領域分割のためプラグインが導入されている．ここでは，もっと単純な閾値による分割，インタラクティブなGraph Cutによる分割とLevel Setによる分割を紹介する．

1.1 閾値

撮影条件が良ければ閾値による分割で十分．

1.2 Graph Cut

Graph Cutはデータ項（入力画像への近さ）と平滑化項（隣接するピクセルでの変化の小ささ）からなるエネルギー関数を大域的に最小化する手法．以下の手順でおこなう．

メニューバーから「Plugins」→「Segmentation」→「Trainable Weka Segmentation」を開く
適当な選択ツール（Freehand Lineツールなど）で注目領域(今回は葉の領域)とそれ以外をそれぞれclass 1とclass 2に指定する
選び終わったら「Train classifier」を押し，判別器の学習を行う
- 今回は既に学習済みの判別器を用意しているのでそれを利用しても良い（ij/classifiler_01.model,ij/classifiler_02.model）
- その場合は，「Load classifier」から好きな判別器を選択する
学習が終わると「Get probability」が実行可能になるので押す
- 先程の各classに属する確率を画素値とした画像スタック「Probability maps」が得られる
この Probability mapsを選択した状態で「Plugins」→「Segmentation」→「Graph Cut」を開き，分割したいチャンネル（今回は，葉として指定したclass 1に対応する 1）を選択する
Graph Cut のウィンドウが開くので，「Segment image」を押す．領域の分割がおこなわれる．
- 結果は二値画像として表示される．今回は輪郭形状をシャープに抽出するためSmoothnessのパラメータを低めに設定する．

1.3 Level Set

これらの他にもFijiには領域分割のためのプラグインが複数ある．「Plugin」→「Segmentation」で利用できるので試してみて欲しい．

2. 輪郭抽出

「Manage update sites」を押し，Manage update sites のウィンドウを開きます．Biomedgroupにチェックを入れ，「Add update site」を押し追加します．最後に，ImageJ Updaterウィンドウで「Apply changes」ボタンを押し，Biomedgroupのライブラリ群を導入し，Fijiを再起動します．これで，IJ Blobライブラリが利用可能になりました．

Rでの輪郭形状解析と統計処理

スクリプト全体はefa.rを参照．

Momocsを読み込み，Rでの解析を始める．繰り返すが，Momocsは現在も開発が進行中であり，開発者も最新版をインストールすることを推奨している．そのため今回も最新版を導入する．

# MomocsをGitHubから導入
devtools::install_github("vbonhomme/Momocs", build_vignettes= TRUE)
# Momocsのロード
library(Momocs)

また，データを読み込む．予め用意してあるデータでも，これまでにFijiで作成したデータでも良い．以下の例では，予め準備してあるデータ（coord）を利用している．

# -- 輪郭データ準備 -- #
# データの一括読み込み
coordDir <- "./coord"
coordFiles <- list.files(coordDir)
coordFiles <- grep('^[0-9a-z]+_[0-9]+.csv$',coordFiles,value=TRUE)
coordFiles <- sapply(coordFiles,function(x) {paste(coordDir,x,sep="/")})
coordData <- import_txt(coordFiles, header=FALSE, sep=",",col.names=c("x","y"))

# 座標データを輪郭形式に変換
grapevine <- coo_close(Out(coordData))

# データの表示
stack(grapevine)

このような図が表示される．

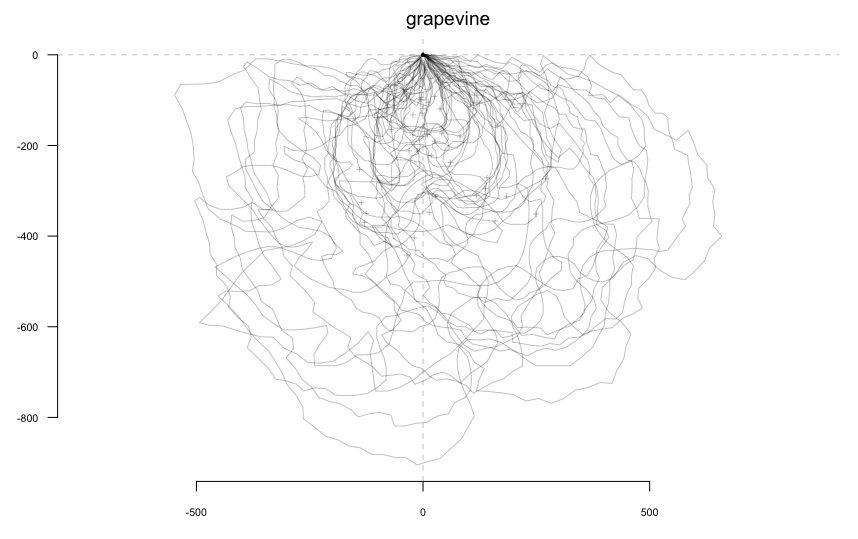
0. 輪郭抽出

既にFijiを利用して輪郭抽出は完了している．しかし，Momocsにも輪郭抽出機能がある．極めて簡単に利用できるので紹介する．

# -- 輪郭データ準備 -- #
# 画像データの一括読み込み
imgDir <- "./img/binarized"
imgFiles <- list.files(imgDir)
imgFiles <- grep('^[0-9a-z]+.jpg$',imgFiles,value=TRUE)
imgFiles <- sapply(imgFiles,function(x) {paste(imgDir,x,sep="/")})
imgData <- import_jpg(imgFiles)

# 座標データを輪郭形式に変換
grapevine <- coo_close(Out(imgData))

# データの表示
stack(grapevine)

閾値による二値化とそこからの輪郭抽出をおこなっているらしい（Extracts outline coordinates from a single .jpg file，Extracts outline coordinates from multiple .jpg files）．

どうも今回の画像からはすべての葉を抽出できなかったようだ．

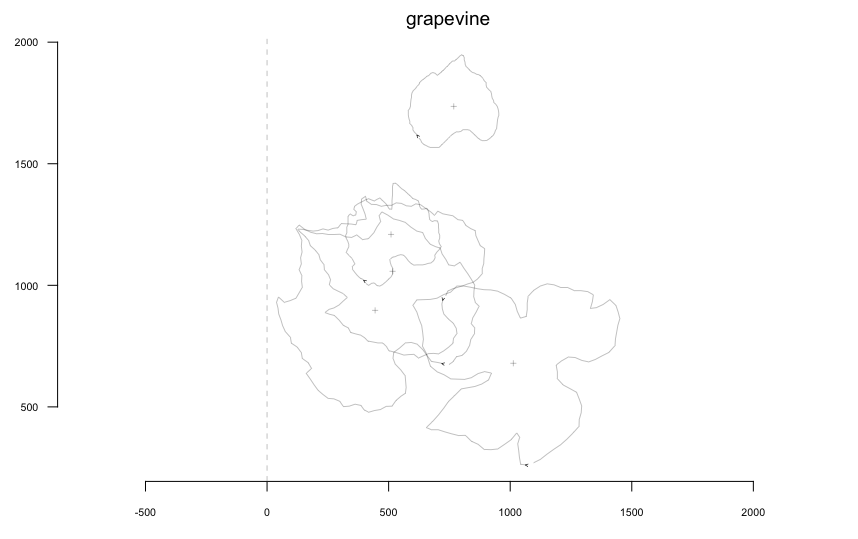
1. 楕円フーリエ解析

まずデータの位置合わせ（registration）をおこなう．

# 規格化
# 位置
grapevine.preform <- coo_center(grapevine)
# サイズ
grapevine.preshape <- Out(sapply(grapevine.preform$coo, function(x){x/sqrt(coo_area(x))}))
# 向き
grapevine.shape <- coo_align(grapevine.preshape)
grapevine.shape <- coo_slidedirection(grapevine.shape, "E")

# データの一覧を表示
panel(grapevine.shape,names = TRUE)

さらに微調整する．

# 再配値
grapevine.shape.realign <- replaceBatch(replaceList, grapevine.shape)
# 全体の確認
panel(grapevine.shape.realign,names = TRUE)

replaceBatchは向きを調整したい標本のインデックスと回転角のペアのリスト（replaceList）を指定することで，再配置したOutを返す関数．詳細はefa.rを参照．

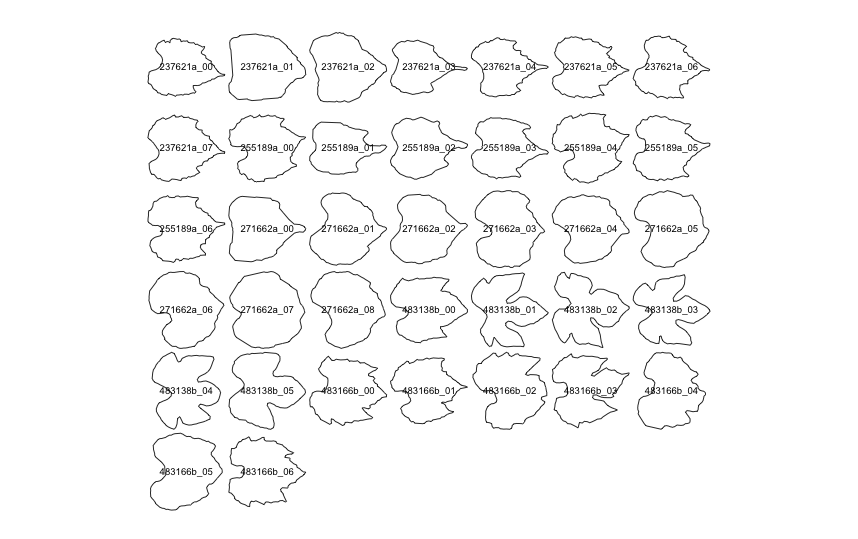
あとは楕円フーリエ解析で，x座標，y座標それぞれの軌跡におけるフーリエ係数を計算する．

# 楕円フーリエ解析
# 今回は既に規格化しているのでnormオプションをFALSEにしている
grapevine.efc <-efourier(grapevine.shape.realign, 100, norm = FALSE)

2. 主成分分析

結果を見ていこう．よくおこなわれるのは主成分分析による縮約と各主成分の寄与率を計算することだ．

# 主成分分析
grapevine.pca <- PCA(grapevine.efc)

# PCAの結果の可視化
plot(grapevine.pca)
plot3(grapevine.pca)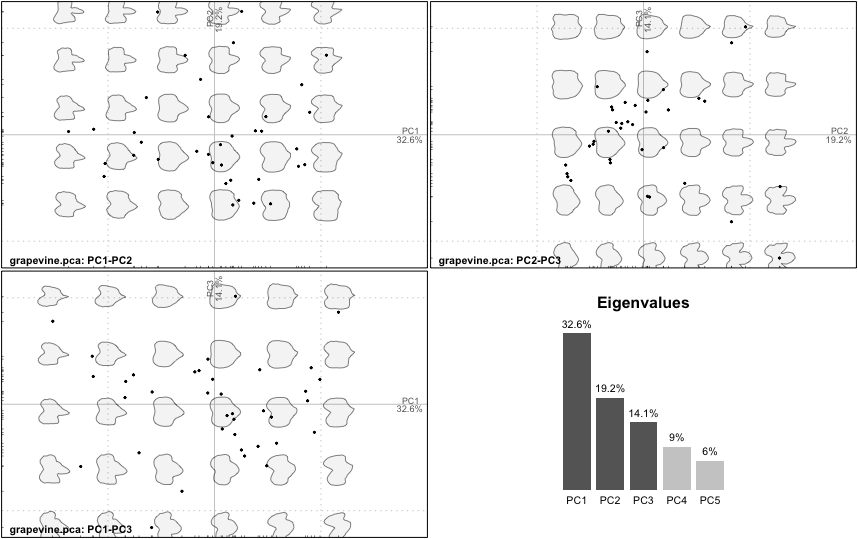

各軸の変化も確認してみよう．

# 主成分軸に沿った形状の変化
PCcontrib(grapevine.pca)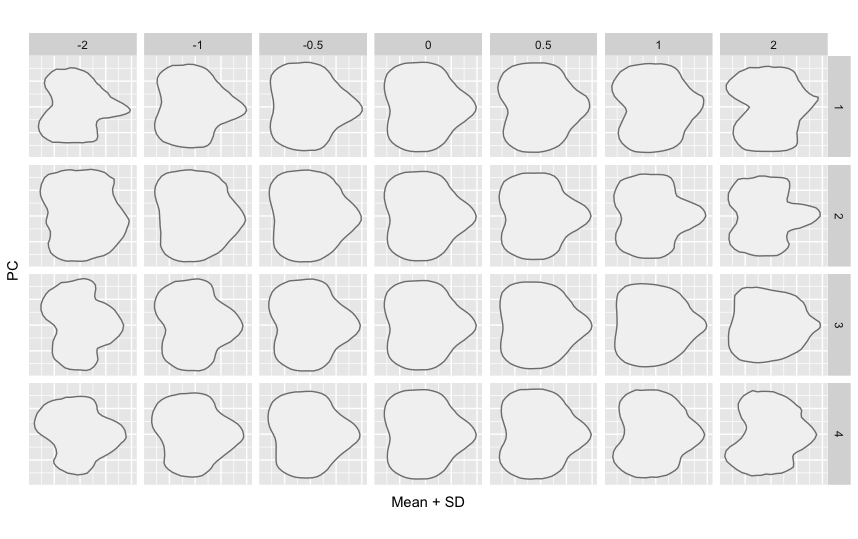

3. 形状の再構築

逆にフーリエ係数のセットから形状を構築できる．ここでは，一枚の葉のオリジナルの座標値（grapavine.shape.realign）とパラメタライズされたフーリエ係数から再構築された形状（grapavine.efi）を比較してみる．

# 輪郭形状の再構築
grapevine.efi <- as.Out(grapevine.efc)

# 再構築した輪郭の可視化
index <- [num]
coo_plot(grapavine.shape.realign[index])
coo_draw(grapavine.efi[index], border='red', col=NA)

numは可視化したい標本のインデックス．

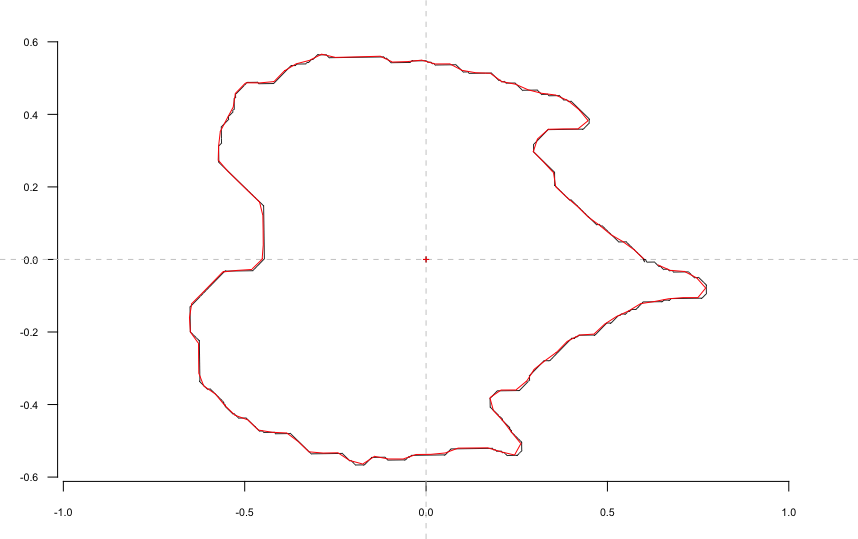
黒がオリジナルの座標値，赤が再構築された形状をそれぞれあらわす．

もう少し踏み込んだ解析

本節は加筆中です．しばらくお待ち下さい．

楕円フーリエ解析で輪郭形状を定量化・再構築できることがわかりました．
しかし，それだけで科学的に面白い知見が得られる訳ではありません．

以下では，幾つかのもう少し踏み込んだ解析例を紹介します．

育種学会2015秋　若手の会ワークショップ

葉の輪郭形状解析

使うツールやデータ

Fiji

R

Momocs

サンプルデータ

解析手順

準備

Fijiでの前処理

1. 領域分割と二値化

1.1 閾値

1.2 Graph Cut

1.3 Level Set

2. 輪郭抽出

Rでの輪郭形状解析と統計処理

0. 輪郭抽出

1. 楕円フーリエ解析

2. 主成分分析

3. 形状の再構築

もう少し踏み込んだ解析

輪郭形状の左右成分の分離

種間での輪郭形状差の検出

左右・遠位-近位での輪郭形状差の検出

成長に伴う輪郭形状の変化

GWASやGSへの応用

参考文献

リンク

育種学会2015秋 若手の会ワークショップ

葉の輪郭形状解析

使うツールやデータ

Fiji

R

Momocs

サンプルデータ

解析手順

準備

Fijiでの前処理

1. 領域分割と二値化

1.1 閾値

1.2 Graph Cut

1.3 Level Set

2. 輪郭抽出

Rでの輪郭形状解析と統計処理

0. 輪郭抽出

1. 楕円フーリエ解析

2. 主成分分析

3. 形状の再構築

もう少し踏み込んだ解析

輪郭形状の左右成分の分離

種間での輪郭形状差の検出

左右・遠位-近位での輪郭形状差の検出

成長に伴う輪郭形状の変化

GWASやGSへの応用

参考文献

リンク

育種学会2015秋　若手の会ワークショップ