"巻き"の理論形態モデル（１）：対数らせんモデル

“巻き"の数理モデル

　これから数回に分けて"巻き"の理論形態モデルをいくつか紹介したい． 基本的には，数理生物学会ニュースレターの第83号の野下(2017)の内容をベースにするつもりだが，追加の内容を盛り込んだり，図を増やしたり，サンプルコードを公開したりする予定．

貝殻と付加成長

　基本的に軟体動物のつくる貝殻を想定してモデルを紹介していく． 最終的には紹介するモデルは，より一般の３次元的な管状構造（“太さを持った空間曲線”）や付加成長する物体についても拡張できるのだが， 当面は貝殻のかたちと成長を記述するモデルとしての側面から紹介していきたい．

　まず軟体動物の貝殻がどのように作られるのかを確認したい． 軟体動物の殻は，炭酸カルシウムを主な成分として生物が自身でつくる生体鉱物（biomineral）である． 内臓塊を覆う器官である外套膜の辺縁部（外套膜縁）で， まず有機物からなる膜状構造（殻皮）を殻表面に形成し，これを基質に炭酸カルシウムの結晶を沈着させ殻層が成長してゆく．

このように殻口の"縁” へ少しづつ沈着させることで殻を成長させる「付加成長」と呼ばれる成長様式をとる．

例えば腹足類の場合は，巻きの中心に対して殻口の外側が内側に対して大きく成長することで，殻が巻くことになる（図1）．

これから紹介していくモデルは，この形作りの仮定を（程度の差はあるが）反映している．

対数らせんモデル logarithmic spiral model

最もシンプルな巻きパタンのモデルとして対数らせんモデル¹から見ていこう．

ここでは極座標系を考えて，動径$r$と偏角$\theta$に以下の関係があるとしよう． $$ \begin{equation} \frac{d r}{d \theta} = \alpha r(\theta) \label{eq:ls}\tag{1} \end{equation} $$

$\alpha$は成長率を定めるパラメータである． $r$（巻きの中心から殻口の端までの長さ）がある種の体サイズを表していると考えれば，その成長速度は体サイズに比例することを表現している²．

式（\ref{eq:ls}）を初期条件$r(0) = r_0$として解けば， $$ r(\theta) = r_0 e^{\alpha \theta} \label{eq:lssol}\tag{2} $$ となり，この平面曲線は対数らせんとなる．

成長率を定めるパラメータ$\alpha$を変化させると様々な巻きパタンを描ける（図2）．

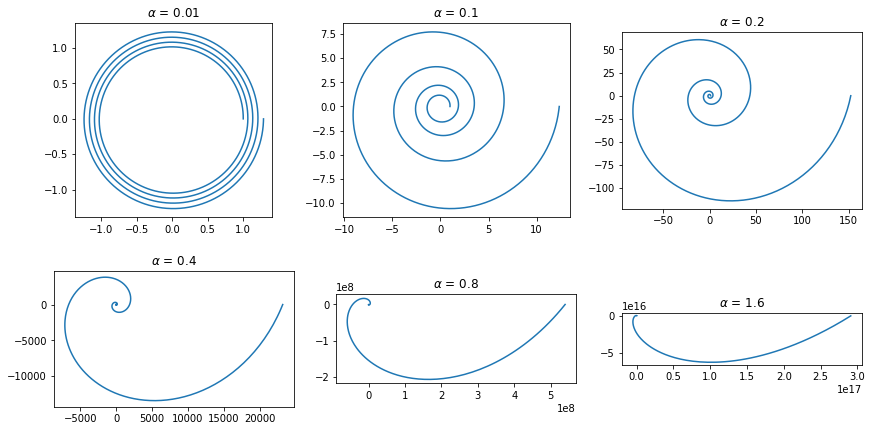
サンプルコード

実際に動かしてみたい方はサンプルノートブックをダウンロードして or Colab上で試してみて！

問題点を発見した場合はissueの投稿をお願いします🙇

次回予告

対数らせんモデルはなかなかに多様な巻きパタンを記述できることがわかった． しかし，やはり太さを持った管である螺管が３次元的に巻いている実際の貝殻を記述するにはいささか表現力が足りない．

次回は，理論形態学という分野が生まれる契機となったRaupのモデルについて紹介したい．

参考文献

• Moseley H, 1838. XVII. On the geometrical forms of turbinated and discoid shells. Philosophical Transactions of the Royal Society of London 128, 351–370. https://doi.org/10.1098/rstl.1838.0018
• Thompson D’Arcy Wentworth, 1992. On Growth and Form, Revised. ed. Dover Publications, New York.
• Thompson D’Arcy Wentworth, 1942. On Growth and Form, 2nd ed. Cambridge University Press.
• 野下浩司, 2017. 巻きの理論形態モデル：有殻軟体動物を例に. 日本数理生物学会ニュースレター 83, 19–23.